ΠΟΛΙΤΙΣΜΟΣ ΚΑΙ ΜΟΥΣΙΚΗ: ΗΧΟΣ - Ο ΓΗΙΝΟΣ ΠΟΛΙΤΙΣΜΟΣ

Τι είναι ήχος?

Ήχος, είναι μια μορφή ενέργειας ,είναι παλμικές δονήσεις που παράγονται από ένα σώμα όταν αύτο τεθεί σε κίνηση,ταλάντωση κτλ.
Για τη μετάδοση των ηχητικών κυμάτων είναι απαραίτητη η ύπαρξη κάποιου υλικού μέσου μεταξύ πομπού και δέκτη. Το μέσο μπορεί να βρίσκεται σε οποιαδήποτε κατάσταση ύλης - στερεό, υγρό, αέριο ή πλάσμα. Βασική προυποθεση ύπαρξης ήχου ειναι ο αέρας - καθώς ο ήχος δεν διαδίδεται στο απόλυτο κενό.

Όταν, εξαιτίας κάποιου ερεθίσματος, δημιουργηθεί μια μορφή διατάραξης στο υλικό μέσο, τότε τα μετατοπισμένα μόρια ύλης ασκούν δυνάμεις στα γειτονικά μόρια, αναγκάζοντάς τα να έλθουν εκτός θέσης ισορροπίας. Με αυτό τον τρόπο η διατάραξη ταξιδεύει στο μέσο - το φαινόμενο ονομάζεται διάδοση.

Πώς ακούμε ?

Η παρουσία της ακοής, στα πλαίσια ενός υγιούς οργανισμού, είναι πάντοτε δυνατή - σε αντίθεση με την όραση.

Επιπλέον, ο ήχος παράγεται κυρίως από τους ζωντανούς οργανισμούς, είτε από το αναπνευστικό σύστημά τους και το λαρύγγι τους ως φωνή, είτε εξαιτίας της κίνησής τους.

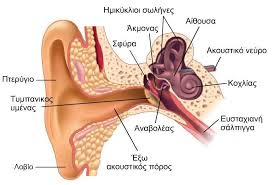
Το αυτί αποτελείται από τρία κύρια μέρη, το καθένα από τα οποία είναι ζωτικής σημασίας στη λήψη και στην ερμηνεία του ήχου.

Έξω αυτί - το εξωτερικό αυτί συλλέγει τον ήχο στην κόγχη και τον μεταφέρει κατά μήκος του ακουστικού πόρου

Μέσο αυτί - οι ήχοι δονούν το τύμπανο του αυτιού το οποίο με την σειρά του κινεί τα τρία οστά που βρίσκονται στο μέσο αυτί

Έσω αυτί - η κίνηση αυτή μεταδίδει δονήσεις στον κοχλία του εσωτερικού αυτιού, μέσω εύθραυστων τριχοφόρων κυττάρων που μετατρέπουν την δόνηση σε νευρικά ερεθίσματα τα οποία στη συνέχεια μεταδίδονται από το εσωτερικό νεύρο στον εγκέφαλο για αναγνώριση. Οι υποδοχείς ενεργοποιούνται ανάλογα με το ύψος και την ακουστικότητα του ήχου και στέλνουν ηλεκτρικά ερεθίσματα στον εγκέφαλο. Όλα αυτά τα ερεθίσματα διαμορφώνουν μία ακαθόριστη σύνθεση ήχων.

Οτιδήποτε διαταράσσει αυτή τη λεπτή λειτουργία θα προκαλέσει απώλεια ακοής.

Για να καταλάβουμε πώς μπορούν να βλάψουν οι δυνατοί ήχοι την ακοή μας, ας εξετάσουμε τον εξής παραλληλισμό. Aς συγκρίνουμε τα τριχοκύτταρα του εσωτερικού αφτιού(αυτιού) με το σιτάρι σε ένα χωράφι, και τον ήχο που μπαίνει στο αφτί με τον άνεμο. Το απαλό αεράκι, όπως ένας χαμηλός ήχος, θα κουνήσει τις κορυφές του σιταριού, αλλά το σιτάρι δεν θα πάθει ζημιά. Εντούτοις, αν αυξηθεί η ταχύτητα του ανέμου, θα αυξηθεί και η πίεση που ασκείται στο στέλεχος του σιταριού. Ένας ξαφνικός, πολύ δυνατός άνεμος ή η συνεχής έκθεση σε χαμηλότερους ανέμους για μεγάλη περίοδο χρόνου μπορεί να βλάψει ανεπανόρθωτα το στέλεχος καταστρέφοντάς το.

Κάτι παρόμοιο συμβαίνει με το θόρυβο και τα μικροσκοπικά, ευαίσθητα τριχοκύτταρα του εσωτερικού αφτιού. Ένας στιγμιαίος, δυνατός θόρυβος μπορεί να καταστρέψει τους ιστούς του εσωτερικού αφτιού και να προξενήσει βλάβη που θα οδηγήσει σε μόνιμη απώλεια ακοής. Επιπλέον, τα παρατεταμένα επικίνδυνα επίπεδα θορύβου μπορούν να βλάψουν μόνιμα τα ευαίσθητα τριχοκύτταρα. Αν συμβεί αυτό, τότε τα τριχοκύτταρα δεν θα μπορέσουν να αναπαραχθούν. Το επακόλουθο αποτέλεσμα ίσως είναι ο βόμβος—το βούισμα, το κουδούνισμα ή ο βρυχηθμός στα αφτιά ή στο κεφάλι.

Όσον αφορά τον τρόπο με τον οποίο ακούμε, όχι μόνο τη μουσική αλλά όλους τους ήχους και τους θορύβους, οι ερευνητές θεωρούν ότι η εισροή των ηχητικών ερεθισμάτων φθάνει αρχικά σε κάποιους νευρώνες οι οποίοι βρίσκονται πιο έξω στον εγκέφαλο, τους εξωτερικούς αισθητικούς νευρώνες, όπως τους ονομάζουν. Οταν αυτοί διεγείρονται, η εκροή των δεδομένων τους πηγαίνει σε κάποιους άλλους, «εσωτερικούς» νευρώνες, οι οποίοι στη συνέχεια διαβιβάζουν το σήμα στα κατάλληλα κέντρα του εγκεφάλου.

«Εκείνο το οποίο συνειδητοποιήσαμε, αναλυτικά και με προσομοιώσεις, αλλά κυρίως με την αναλυτική παραγωγή, είναι ότι η κατανομή των παλμών στην εκροή είναι πολύ πιο ομαλή όταν οι ήχοι είναι αρμονικοί σε σχέση με όταν είναι δυσαρμονικοί»
Η οικογένεια των επιστημών που ασχολείται με τη βιολογική διάσταση της ακοής ονομάζεται auditory science .

ΔΙΑΜΗΚΗ ΚΥΜΑΤΑ

ΕΓΚΑΡΣΙΑ ΚΥΜΑΤΑ

Εγκάρσια κύματα ονομάζονται τα κύματα των οποίων η διεύθυνση διάδοσής τους είναι κάθετη στη διεύθυνση της ταλάντωσης των σωματιδίων που αποτελούν το μέσο διάδοσης.

Διαμήκη κύματα ονομάζονται τα κύματα των οποίων η διεύθυνση διάδοσής τους είναι παράλληλη στη διεύθυνση της ταλάντωσης των σωματιδίων που αποτελούν το μέσο διάδοσης.

Η ΙΣΤΟΡΙΑ ΜΙΑ ΧΟΡΔΗΣ

Οι Κινέζοι και οι αρχαίοι έλληνες πειραματίστηκαν πολύ με τις χορδές. Είχαν διαπιστώσει πως όσο πιο απλός είναι ο λόγος ίδιων χορδών διαφορετικού μήκους , τόσο πιο σύμφωνες είναι οι χορδές μεταξύ τους ( πχ: 2/1, 3/2. βλ πυθαγόρεια κλίμακα). Επειδή δε γνώριζαν την ύπαρξη των αρμονικών δε μπορούσαν να δώσουν μια επιστημονική εξήγηση σε αυτό το φαινόμενο κι έτσι κατέφυγαν σε μυστικιστικές εξηγήσεις. Αργότερα ο Κλαύδιος Πτολεμαίος(127-151μΧ) επινόησε ένα σύστημα κουρδίσματος κατά το οποίο όλα τα διαστήματα παράγονταν από τις 8ες, τις καθαρές (φυσικές) 5ες και ορισμένες καθαρές (φυσικές) μεγάλες 3ες. Αυτό το σύστημα ονομάστηκε από τους μεταγενέστερους just intonation.

Το κούρδισμα των χορδών με βάση τους πολύ απλούς λόγους επεκράτησε έως το μεσαίωνα. (Για τα φυσικά διαστήματα θυμίζουμε ότι: ο λόγος 2/1 δίνει την οκτάβα και ο λόγος 3/2 την πέμπτη καθαρή. 4/3= τέταρτη καθαρή. 5/4 =τρίτη μεγάλη 6/5= τρίτη μικρή).
Μιλώντας με σημερινούς όρους , το πυθαγόρειο κούρδισμα και το just intonation στηρίζονται στα εξής:

Υπόηχοι : ήχοι που βρίσκονται μεταξύ του κατώτατου ορίου της ανθρώπινης ακοής (20 Hz) έως συχνότητες 0,001 Hz. Αυτή η περιοχή του ακουστικού φάσματος χρησιμοποιείται στη σεισμολογία για την παρακολούθηση των σεισμών. Οι υπόηχοι μπορούν να διαδοθούν σε μεγάλες αποστάσεις, ειδικά μέσα σε στερεά ή υγρά μέσα και να παρακάμψουν εμπόδια χωρίς σημαντική εξασθένιση.

Υπέρηχοι : ήχοι που βρίσκονται μεταξύ του ανώτερου ορίου της ανθρώπινης ακοής ,με συχνότητα μεγαλύτερη από αυτήν που μπορεί να ακούσει ο άνθρωπος (περίπου 20.000 Hz). Με άλλα λόγια ο υπέρηχος είναι ένας ήχος τόσο ψηλός που δεν μπορούμε να τον ακούσουμε, καθώς το ανθρώπινο αυτί έχει κάποια όρια και δεν μπορεί να ακούσει πολύ ψηλούς ή χαμηλούς ήχους. Ωστόσο, άλλα ζώα είναι ικανά να ακούσουν υπερήχους, όπως ο σκύλος, ενώ οι νυχτερίδες χρησιμοποιούν για να "βλέπουν" την νύχτα

Πατέντα προσομοίωσης κυμάτων ήχου New York (1960)

Η συχνότητα ταλάντωσης μιας χορδής είναι αντιστρόφως ανάλογη με το μήκος της . Πχ: Αν μία χορδή μήκους ενός μέτρου δίνει έναν ήχο με συχνότητα 600 κύκλων ( ταλαντώσεων) το δευτερόλεπτο (600 Hz), η ίδια χορδή με το μισό μήκος (50 εκατοστά) μας δίνει έναν ήχο με συχνότητα 600 Χ 2 = 1200 κύκλους το δευτερόλεπτο (1200 Hz). Η ίδια χορδή με μήκος 2/3 του μέτρου παράγει ήχο με συχνότητα 600 X 3/2 = 900 Hz, κλπ.

Ο παραπάνω κανόνας ισχύει κάτω από συγκεκριμένες προϋποθέσεις:

1) Ο ήχος παράγεται από χορδή.

2) Παράγεται από την ίδια χορδή ( ίδιο υλικό, πάχος , τέντωμα).

Για να εξετάσουμε την κατασκευή μουσικών διαστημάτων ανεξάρτητα από το αν χρησιμοποιούμε χορδή ή σωλήνα, χρειαζόμαστε ένα πιο γενικό κανόνα ο οποίος χρησιμοποιεί τη συχνότητα (συχνότητα: ο αριθμός ταλαντώσεων ενός σώματος ανά δευτερόλεπτο).

Η βασική αρχή έχει ως εξής:
Αν η συχνότητα ενός τόνου είναι n, τότε η συχνότητα της οκτάβας του είναι 2n, η συχνότητα της 5ης είναι ( 3/2)n, και της 3ης μεγάλης είναι ( 5/4)n.
Από αυτούς τους τόνους προκύπτουν όλοι οι υπόλοιποι της διατονικής κλίμακας.Κανένα μουσικό όργανο δεν παράγει απόλυτα " καθαρούς" ήχους. Στην πραγματικότητα κάθε μουσικός ήχος είναι η ταυτόχρονη παραγωγή πολλών σχετικών (μεταξύ τους), καθαρών ήχων: του θεμέλιου (fundamental) με συχνότητα f, και των αρμονικών ( overtones ή harmonics) με συχνότητες πολλαπλάσιες από αυτή του θεμέλιου, δηλαδή 2f, 3f, 4f κλπ.

ΟΙ ΑΡΜΟΝΙΚΟΙ

    Οι αρμονικοί μέσα στο μουσικό ήχο διαφέρουν ως προς την ένταση (loudness): ορισμένοι μπορεί να έχουν πολύ χαμηλή ένταση ή , ακόμη και, να απουσιάζουν, ενώ μερικοί μπορεί να είναι πιο δυνατοί ακόμη και από το θεμέλιο.
   Η αναλογία του θεμέλιου ήχου και των αρμόνικων στη συνολική ένταση, μας δίνει την αίσθηση της χροιάς του ήχου(timbre). Η χροιά δε διαφοροποιείται και τόσο μεταξύ των διαφορετικών φθόγγων στα όργανα ίδιου τύπου, όμως διαφοροποιείται μεταξύ οργάνων διαφορετικού τύπου. Η χροιά είναι αυτή που μας επιτρέπει να ξεχωρίσουμε αν ένας φθόγγος παίζεται από βιολί ή ( ο ίδιος φθόγγος) από φλάουτο.

Eπιστήμες του ήχου

Η επιστήμη που ασχολείται με τη φυσική διάσταση του ήχου είναι η φυσική ακουστική "acoustics" . Ο ήχος ως φυσικό φαινόμενο απασχολεί τους ανθρώπους από τα αρχαία χρόνια. Στο πέμπτο βιβλίο του Βιτρούβιου, από τα δέκα του έργου του " περί αρχιτεκτονικής" ( De Architectura) αναφέρεται ότι οι αρχαίοι έλληνες κατασκεύαζαν βάζα με διαστάσεις και αναλογίες τέτοιες ώστε να μπορούν να χρησιμοποιηθούν ως αντηχεία στο θέατρο. (Marcus Vitruvius Pollio: περίπου 80-70 πΧ έως 15 πΧ).
Οι μεταγενέστεροι κατασκευαστές ναών "εμφύτευαν" στα θολωτά μέρη του ναού στάμνες με το στόμιό τους στραμμένο προς το χώρο του ναού. Με τα αντηχεία αυτά πειραματίστηκε πολύ αργότερα ο Helmholtz από τον οποίο πήραν το όνομά τους: αντηχεία Helmholtz.

To μαθηματικό υπόβαθρο της φυσικής ακουστικής τέθηκε το 17ο αιώνα . Τότε διατυπώθηκε η έννοια του λογάριθμου και του απειροστικού λογισμού ( calculus) .

Εκείνη την περίοδο επίσης το φως και ο ήχος παρουσιάστηκαν ως ημιτονοειδή σήματα (sine waves).

20Hz to 20kHz (Human Audio Spectrum)

Συγκερασμός

Equal temperament

Στη δυτική μουσική ο συγκερασμός (temperament or intonation) είναι ο τρόπος με τον οποίο η οκτάβα υποδιαιρείται σε 12 όμοια ''ακουστικά μέρη''.

Είναι αυτό που γνωρίζουν οι περισσότεροι άνθρωποι σήμερα . Μια οκτάβα υποδιαιρείται σε 12 ίσα μεταξύ τους ημιτόνια

.
Για την υποδιαίρεση της οκτάβας σε 12 ίσα μέρη (δηλαδή τα ημιτόνια) απαιτούνται πολύπλοκα μαθηματικά τα οποία μπορούν να απλοποιηθούν με τη χρήση των λογάριθμων. θυμίζουμε ότι λογάριθμος ( log) με βάση ψ ενός αριθμού Χ είναι η δύναμη στην οποία υψώνεται ένας αριθμός- βάση( Ψ) για να μας δώσει το Χ. π.χ. όταν έχουμε βάση το 10: log(100)= 2 , επειδή 102=100. Είναι πιο πρακτικό να εργάζεται κάποιος με το λογάριθμο του λόγου των συχνοτήτων από ότι με τον ίδιο το λόγο των συχνοτήτων.

Το cent που είναι λογαριθμική μονάδα μέτρησης, χρησιμοποιείται για τη μέτρηση των διαστημάτων. Ο λόγος του είναι 1/1200 μιας οκτάβας.

Μία οκτάβα έχει 1200 cents: κάθε ημιτόνιο έχει 100 cents. Μια 5η καθαρή = 7 ημιτόνια=700 cents.

Η αρμονία στη μουσική και ο τρόπος με τον οποίο μπορούμε να την εντοπίζουμε σχεδόν πάντα είναι ένα «μυστήριο» που έχει απασχολήσει φιλοσόφους και επιστήμονες από την Αρχαιότητα. Τώρα μια ομάδα φυσικών πιστεύει ότι βρήκε τη λύση του: κρύβεται, όπως υποστηρίζει, στην εντροπία των σημάτων που στέλνουν οι νευρώνες του ακουστικού συστήματος στον εγκέφαλό μας.

Το «κλειδί» στις συχνότητες

Πολλές θεωρίες έχουν προταθεί ως τώρα για να εξηγήσουν γιατί αντιλαμβανόμαστε ορισμένους συνδυασμούς ήχων – όπως, π.χ., μια συγχορδία από νότες ή ένα τραγούδι που εκτελείται με συνοδεία μουσικών οργάνων ή από περισσότερες από μία φωνές – ως ευχάριστους και άλλους ως δυσάρεστους. Καμία όμως δεν έχει βρει μια απόλυτα ικανοποιητική απάντηση.

Ο Μπερνάρντο Σπανιόλο, καθηγητής Φυσικής στο Πανεπιστήμιο του Παλέρμο στην Ιταλία, μαζί με τον Γιούρι Ουσάκοφ και τον Αλεξάντρ Ντουμπκόφ του τμήματος Ραδιοφυσικής του Πανεπιστημίου Λομπασέφσκι του Νίζνι - Νόβγκοροντ, στη Ρωσία, προτείνουν μια εντελώς καινούργια ιδέα. Σύμφωνα με τη μελέτη τους, η οποία δημοσιεύθηκε στην επιθεώρηση «Physical Review Letters», το ευχάριστο ή μη άκουσμα των ήχων εξαρτάται από τη συχνότητά τους – ή- ακριβέστερα, από τον συνδυασμό των συχνοτήτων τους και τους παλμούς που αυτοί προκαλούν στους νευρώνες μας.

«Σε μια συγχορδία έχουμε τη σύνθεση δύο τόνων, δύο διαφορετικών αρμονικών ταλαντώσεων που η καθεμιά τους έχει διαφορετική συχνότητα», εξηγεί μιλώντας στο «Βήμα» ο Μπερνάρντο Σπανιόλο. «Οταν η συγχορδία είναι αρμονική, δηλαδή ευχάριστη, είδαμε ότι ο λόγος μεταξύ αυτών των συχνοτήτων αποτελείται από μικρούς σε μέγεθος φυσικούς αριθμούς. Παραδείγματος χάριν, 2 προς 3, 4 προς 5, 3 προς 2 – πάντως σε γενικές γραμμές μικρότερους του δέκα». Αντιθέτως, όσο πιο δυσαρμονική είναι η συγχορδία, τόσο πιο «μεγάλα» είναι τα ψηφία των συντελεστών αυτής της αναλογίας – χαρακτηρίζονται συνήθως, όπως εξηγεί, από αριθμούς όπως 45 προς 42, 37 προς 35 και αντιστρόφως.....

Πώς λειτουργούν οι «αισθητικοί» νευρώνες

Ο πρώτος που αναγνώρισε την «αριθμητική» αντίληψη της μουσικής ήταν, όπως λέει ο καθηγητής, ο Πυθαγόρας. «Την εποχή εκείνη φυσικά δεν υπήρχε μουσική σαν του Μπετόβεν ή του Μότσαρτ» επισημαίνει. «Επρόκειτο για πολύ απλούς τόνους».

Σήμερα η επιστήμη μπορεί να αναγνωρίζει τις συχνότητες ιδιαίτερα πολύπλοκων ήχων και να καταγράφει τους παλμούς που προκαλούν διεγείροντας τον εγκέφαλο. Αυτήν ακριβώς τη διαδικασία περιγράφει το συγκεκριμένο μοντέλο. Οι ερευνητές «αποκωδικοποιούν» πώς ακριβώς διεξάγεται στο ακουστικό σύστημα του εγκεφάλου μας, υποστηρίζοντας μάλιστα ότι «δεσμεύει» συγκεκριμένα είδη νευρώνων. Τους ονομάζουν «αισθητικούς» νευρώνες και τους χωρίζουν σε «εξωτερικούς» και «εσωτερικούς».

«Οι νευρώνες λειτουργούν σαν ένα σύστημα κατωφλίου» εξηγεί ο καθηγητής .Αυτό σημαίνει ότι όταν κάποια εισροή πληροφοριών φθάνει σε αυτούς, για να διεγερθούν και να προκαλέσουν εκροή πληροφοριών προς άλλα τμήματα του εγκεφάλου -τα ερεθίσματα – τα «εισερχόμενα δεδομένα» – θα πρέπει να βρίσκονται επάνω από κάποιο συγκεκριμένο όριο, κάποιο «κατώφλι». «Αν η εισροή είναι κάτω από το κατώφλι, έχουμε μηδενική εκροή» λέει. «Αν είναι επάνω από το όριο προκαλεί εκροή με τη μορφή μιας αλληλουχίας παλμών. Αυτό σημαίνει ότι είναι σαν μια συσκευή που “αναβοσβήνει”: τη στιγμή που ένας νευρώνας διεγείρεται έχουμε μια αλληλουχία παλμών και μετά, όταν ηρεμεί, η δραστηριότητα είναι μηδενική». Αυτές, λοιπόν,τις αλληλουχίες παλμών εξέτασαν στη μελέτη τους.

Πηγές
1. Claudio Di Veroli :Unequal temperaments, theory, history and practice

2. Tuning and Temperament A Historical Survey J. Murray Barbour
East Lansing Michigan State College Press 1951

3. Willi Apel :Harvard dictionary of music, second edition eighth Printing

>>> Άρχισα να θέλω να κάνω μουσική από πολύ παλιά όταν ήμουνα παιδί. Ξεκίνησα από μια ανησυχία και μια ευαισθησία που είχα βαθύτατη προς τους ήχους. Ασχολήθηκα όμως και με την αρχαιότητα και τη φιλοσοφία, ύστερα έκανα και πολιτική δράση, ασχολήθηκα και με τις επιστήμες. Είχα μπει στο Πολυτεχνείο επειδή με ενδιέφεραν οι επιστήμες και τα μαθηματικά ιδιαίτερα. Στην αρχή, όλα αυτά ήταν ανεξάρτητα μεταξύ τους. Αλλά άρχισα σιγά σιγά να καταλαβαίνω, πως υπήρχε μια πολύ στενή σχέση. Όλοι αυτοί οι τομείς ήταν χοντρικές εκφράσεις της ενότητας του ανθρώπινου μυαλού. Η μουσική είναι και αυτή μια έκφραση, δεν μπορεί παρά να απαρτίζεται από αυτά τα άλλα, τις άλλες εκφράσεις. Επομένως, χωρίς φιλοσοφία, χωρίς μαθηματικά, χωρίς την ιστορία, η μουσική δεν μπορεί να υπάρξει, δεν έχει νόημα. Τα μαθηματικά, άλλωστε, χωρίς μουσική, χωρίς φιλοσοφία, δεν μπορούν να υπάρξουν. Δεν μπορούν να υπάρχουν χωρίς τις εικαστικές τέχνες, χωρίς την τέχνη γενικά Πηγή: www.lifo.gr

https://www.youtube.com/watch?v=Q3oItpVa9fs

Άρχισα να θέλω να κάνω μουσική από πολύ παλιά όταν ήμουνα παιδί. Ξεκίνησα από μια ανησυχία και μια ευαισθησία που είχα βαθύτατη προς τους ήχους. Ασχολήθηκα όμως και με την αρχαιότητα και τη φιλοσοφία, ύστερα έκανα και πολιτική δράση, ασχολήθηκα και με τις επιστήμες. Είχα μπει στο Πολυτεχνείο επειδή με ενδιέφεραν οι επιστήμες και τα μαθηματικά ιδιαίτερα. Στην αρχή, όλα αυτά ήταν ανεξάρτητα μεταξύ τους. Αλλά άρχισα σιγά σιγά να καταλαβαίνω, πως υπήρχε μια πολύ στενή σχέση. Όλοι αυτοί οι τομείς ήταν χοντρικές εκφράσεις της ενότητας του ανθρώπινου μυαλού. Η μουσική είναι και αυτή μια έκφραση, δεν μπορεί παρά να απαρτίζεται από αυτά τα άλλα, τις άλλες εκφράσεις. Επομένως, χωρίς φιλοσοφία, χωρίς μαθηματικά, χωρίς την ιστορία, η μουσική δεν μπορεί να υπάρξει, δεν έχει νόημα. Τα μαθηματικά, άλλωστε, χωρίς μουσική, χωρίς φιλοσοφία, δεν μπορούν να υπάρξουν. Δεν μπορούν να υπάρχουν χωρίς τις εικαστικές τέχνες, χωρίς την τέχνη γενικά. Ίσως αυτή είναι η σπουδαιότερη συνεισφορά μου ή τουλάχιστον ο χώρος στον οποίο δούλεψα τόσα χρόνια. Πηγή: www.lifo.gr

ΠΟΛΙΤΙΣΜΟΣ ΚΑΙ ΜΟΥΣΙΚΗ

ΗΧΟΣ - Ο ΓΗΙΝΟΣ ΠΟΛΙΤΙΣΜΟΣ - Η ΦΥΣΗ ΤΟΥ ΗΧΟΥ

Πώς ακούμε ?

Συγκερασμός

Δεν υπάρχουν σχόλια:

Δημοσίευση σχολίου